All resources of living and non-living provided by nature are called natural resources. In today’s article we are going to know about Optimal depletion of nonrenewable resources. So let’s discuss in details.
Table of Contents
Mention two conditions of Optimal depletion of nonrenewable resources
The nonrenewable resource are those natural resources which can not be generated. As for example- Oil. The non-renewable resource will be depleted so long as the extraction rate is positive. The nonrenewable resource is limited in supply and is not produce able like an ordinary good.
Therefore the extraction (pulling out) and sale of a unit today involves and opportunity cost. This is called user cost (uc). As for example- A barrel of oil extracted today is a barrel unavailable for extraction in the future. Hence we should take into consideration the concept of augmented marginal cost (amc).
The amc is defined as the marginal cost of extraction (mc) + the user cost (uc). In case of ordinary goods the optimum condition requires P = mc. But in case of nonrenewable resources the optimum condition can be written as-
P = mc + uc
⇒ P = amc
This is called first order condition of optimum depletion as given by Hotelling. The current extraction rate by a private owner of a natural resource depends not only on the current price but also on expectations about future prices. Let us assume two periods-
0 = Current period
1 = Future period
P0 = Current Price
P1 = Future Price
C = mc remains constant in both period.
The stock of resource is fixed. Thus amy unit sold in the current period will reduce the quantity that can be sold in future period. If the seller sells the unit in current period he will received net revenue (P0 – C) but forgo revenue of (P1– C) in the future period.
The present value can be calculated as – P1– C/ 1 + r
Where, r is the discount rate. It is the user cost of his decision. It arises because he is faced with the alternative of selling it in the future per hence his return from the selling a unit today will be,
(P0 – C) – P1– C/ 1 + r
If (P0 – C) > P1– C/ 1 + r
The producer will be better of selling his resources in the current period.
If (P0 – C) < P1– C/ 1 + r
He will be better of by leaving the resources in the ground. Therefore, his optimum amount of current extraction is given by –
(P0 – C) = P1– C/ 1 + r —— (i)
⇒ P0 = C + P1- C/ 1 + r —– (ii)
This equation gives us the first order condition of resource depletion. From equation (i) we get-
(P0 – C) = P1– C/ 1 + r
⇒ P0– C/ P1 – C = 1/1 + r
⇒ P1 – C/P0– C = 1 + r
⇒ (P1 – C) = (1 + r) (P0– C)
This is called second order condition of optimal depletion and is usually described as the fundamental equation of exhaustible (non- renewable) resources extraction as given by Hotelling.
Diagram – Optimal depletion of nonrenewable resources
Let us explain the theory with the help of following fig.
In the above figure, on OX axis we measure nonrenewable resource (crude oil) and on OY axis expected price. Extraction leads to exhaustion of the resource if mc = P rule is follow under perfect competition. The crude oil owner expects resource price may rise in future due to resource scarcity.
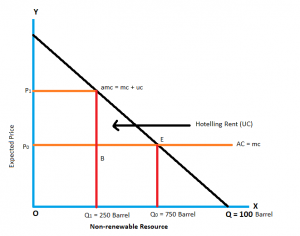
The minimum amount of expected increasing price in future is (P1 – P0) = uc. In the figure P1 > P0, the difference is called user cost (uc) or Hotelling rent. It may be written as P1 = P0 + uc. If future P1 > P0, the resource owner will be prepared to postponed resource extraction.
Conclusion
So friends, this was the concept of Optimal depletion of nonrenewable resources. Hope you get the full details about it and hope you like this article.
If you like this article, share it with your friends and turn on the website Bell icon, so don’t miss any articles in the near future. Because we are bringing you such helpful articles every day. If you have any doubt about this article, you can comment us. Thank You!
Read More Article
• Define Direct tax and Indirect tax | Direct tax and Indirect tax difference
• What is Public Debt? | Types of public debt, Objective
• The ability to pay principle of taxation | Explain critically the principle of the ability to pay
