Hi friends, in today’s article we are going to know about the relationship among AR, MR and Elasticity of demand. So let’s discuss in details.
Table of Contents
Relationship among AR, MR and Elasticity of Demand
There is a crucial relationship between AR, MR and elasticity of demand, which is used extensively in the theory of pricing. The relationship can be explained with the help of following figure –
The actual relationship between AR and MR curve under imperfect competition depends upon the elasticity of the AR ( Average Revenue) curve.
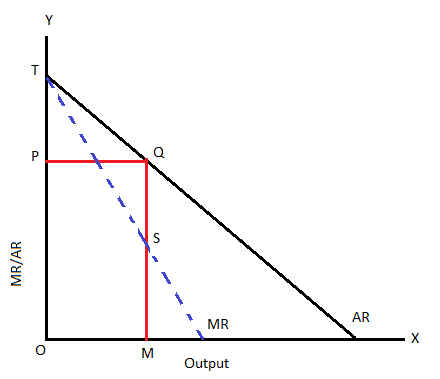
We also new that the price elasticity of demand at a given point on the demand curve can be measured by dividing the lower segment by the upper segment on the demand. That is –
∴ Elasticity of demand (Ep) = Lower segment/Upper segment.
So, in the figure, at point Q, the elasticity of demand is –
E = QM/TP = QM/QS (if TP = QS)
⇒ E = QM/QM – SM = AR/AR – MR [ Here, QM = AR and SM = MR]
∴ E = AR/AR – MR = A/A – M
Where,
A = AR and
M = MR
By solving we have,
EA – EM = A
⇒ EA – A = EM
⇒ A (E – 1) = EM
⇒ A = EM/E – 1
∴ AR = MR (E/E – 1)
Similarly, MR can also be determined
E = A/A – M
By solving, we have
EA – EM = A
– EM = A – EA
M = EA – A/E
or M = A (E – A)/E
Relationship between AR and MR
On the basis of this formula the relationship between AR and MR is established with the help of following figure (A)
At point G on the average revenue curve AR, elasticity of demand is unit, i.e. 1 (One). According to the formula –
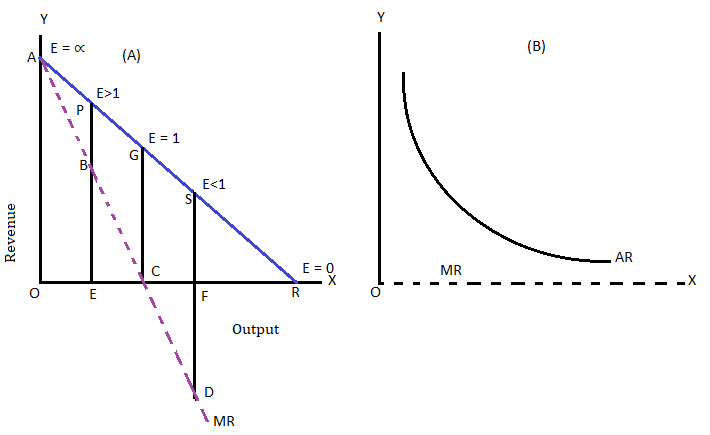
MR = AR (1-1/1) = AR (0/1) = 0
The MR is zero when it touches X axis at point C. Thus, where elasticity of AR curve is unity, MR is zero. If the elasticity of the AR curve is unity through out its length like a rectangular hyperbola, the MR curve will coincide with the X axis shown as dotted line in figure (B).
If the elasticity of the AR curve at point D is greater than unity say 3, then –
MR = AR (3-1/3) = 2/3
It shows that when the elasticity of AR is greater than MR it is always positive, which is PE in figure (A). If the elasticity of AR is less than unity, say ½, MR = AR (½ – 1/½)
= – ½/½ = – 1
It shows MR to be negative. At point S on the AR curve, elasticity is less than unity and MR is negative (FD). If the elasticity of AR is infinity, MR coincides with it at point A in figure (A).
Again, when elasticity of AR is zero, the gap between AR and MR curves becomes wider.
Conclusion
So friends, this was the relationship among AR, MR and Elasticity of demand. Hope you get the full details about it and hope you like this article.
If you like this article, share it with your friends and turn on the website Bell icon, so don’t miss any articles in the near future. Because we are bringing you such helpful articles every day. If you have any doubt about this article, you can comment us. Thank You!
Read More Article
